Universidad Costa Rica

 

 

Escuela Computación e Informática

 

 

Rubén Campos Calderón

 

A41074

 

rubenzion@yahoo.com

 

 

Autómatas y Compiladores

 

CI-1322

 

G1

 

 

Premio 5

 

 

Prof. Adolfo Dimare

 

 

 

17/9/07

 

Transformar un Autómata No Determinista Finito (AFN) a un Autómata Determinista Finito (AFD)

 

 

La idea es tomar los conjuntos de valores de llegada de un estado y agruparlos en un nuevo conjunto, el cual va a ser considerado el nuevo estado de llegada del estado correspondiente.

 

Ejemplo 1

 

Se tiene un AFN, como el que se muestra en la figura

 

 

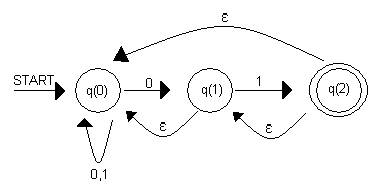
Esta sería su tabla, asociada a los estados

 

	“0”	“1”	“ε”
q0)	{ q(0), q(1) }	{ q(0) }
q(1)		{ q(2) }	{ q(0) }
q(2)			{ q(0), q(1) }

 

 

Primeramente se toma el estado inicial, q(0) y todas las transiciones epsilon (ε) que este tenga, para formar un nuevo conjunto, que vamos a llamar A.

 

Luego se forma el conjunto (llamemos B) que generaría este conjunto A, para el valor de entrada (en este caso 0), más los estados generados por las transiciones ε, en el conjunto recién generado (en este caso de q(0), q(1) )

 

Entonces: q(0) => 0 => { q(0), q(1) } U {  }

                 A    => 0 => { B }

 

También para el valor 1: q(0) => 1 => { q(0) } U {  }

                                          A    => 1 => { A }                       

 

Estos pasos se repiten para todas las entradas del autómata.

 

Ahora se hacen los casos para los conjuntos que se generaron en el paso anterior (en este caso B)

 

{ q(0), q(1) } => 0 => { q(0), q(1) } U {  }

Se genera un nuevo conjunto B = { q(0), q(1) }

                 B    => 0 => { B } 

 

{ q(0), q(1) } => 1 => { q(0), q(2) } U { q(0), q(1) }

Se forma el nuevo conjunto C, que se compone de { q(0), q(1), q(2) } 

                 B    => 1 => { C }

 

Por último como se generó un nuevo conjunto C, se repite el proceso para el este.

 

{ q(0), q(1), q(2) } => 0 => { q(0), q(1) } U { q(0), q(1) }

                 C    => 0 => { B }

 

{ q(0), q(1), q(2) }  => 1 => { q(0), q(2) } U { q(0), q(1) }

                 C    => 1 => { C }

 

Esto se puede representar en una tabla, como se muestra a continuación.

 

	“0”	“1”
A	B	A
B	B	C
C	B	C

 

 

El diagrama de estado correspondiente a este AFD, sería el siguiente

 

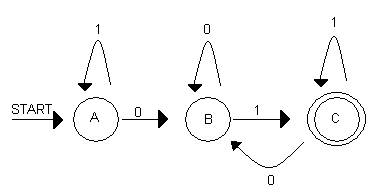
C es se convierte en estado Final, dado que contiene un estado Final del AFN original.

 

Nota: En el paso de incluir las transiciones ε, se deben incluir en “cadena”, todas las transiciones ε asociadas a cada transición ε.

 

 

 

Ejemplo 2

 

Autómata Finito No Determinista

 

 

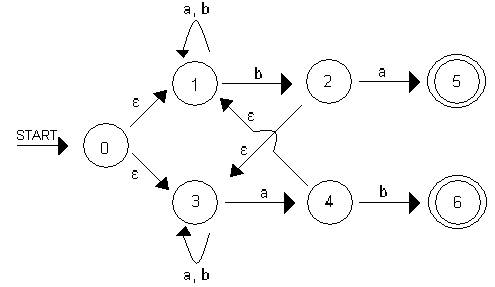
Su tabla asociada.

 

Abreviatura	Conjunto	“a”	“b”
A	[0 1 3]	[1 3 4] + [1]	[1 2 3] + [3]
B	[1 3 4]	[1 3 4] + [1]	[1 2 3 6] + [3]
C	[1 2 3]	[1 3 4 5] + [1]	[1 2 3] + [3]
D	[1 2 3 6]	[1 3 4 5] + [1]	[1 2 3] + [3]
E	[1 3 4 5]	[1 3 4] + [1]	[1 2 3 6] + [3]

 

Los estados Finales, serían aquellos conjuntos que contengan al 5 ó 6

 

Por lo tanto son:

[1 2 3 6] => D

[1 3 4 5] => E

 

Finalmente se tiene una tabla como se presenta a continuación:

 

	“a”	“b”
A	B	C
B	B	D
C	E	C
D	E	C
E	B	D

 

 

Por último este sería el diagrama del autómata finito determinista, generado por el algoritmo de transformación de AFN a AFD

 

 

 

 

 

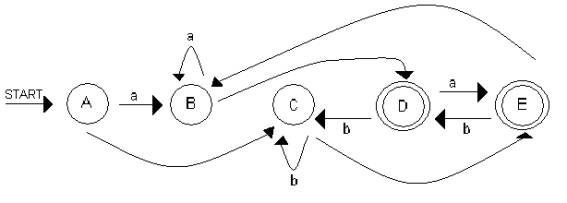
Datos importantes:

 

            Se crean los conjuntos de los posibles estados del autómata No Determinista

 

            Este conjunto es un subconjunto del conjunto de TODOS los estados

 

            Autómata No Determinista => Determinista, si tiene n estados, puede llegar a tener hasta 2^n estados en el autómata determinista.

 

 

 

 

Minimizar un Autómata

 

 

Ejemplo

 

Figura de un AFN

 

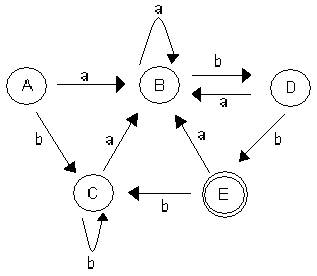
Inicialmente se parten en particiones, que son: Estados Finales y Estados No Finales

 

T(0)     ( A B C D )     ( E )

 

Se trabaja con el conjunto que tiene mas de un elemento

 

Ahora se calculan las transiciones de los estados, con algún valor de entrada del autómata (se escoge a, en este caso)

 

 

	“a”
A	B
B	B
C	B
D	B

 

 

Pero como todos caen en el mismo, pruebo con otro valor (ahora el b)

 

	“b”
A	C
B	D
C	C
D	E

 

Como D genera un valor de otro conjunto, ajeno a él, entonces D se separa en un conjunto aparte.

 

T(1)     ( A B C )         ( D )     ( E )

 

Ahora se repite el proceso

 

	“a”
A	B
B	B
C	B

 

No sirve, voy al siguiente valor

 

	“b”
A	C
B	D
C	C

 

En este caso B genera un valor de otro conjunto ajeno a él, el cual es el D, por lo tanto B se separa en otro conjunto

 

T(2)     (AC)    (B)       (D)       (E)

 

Y se repite el proceso

 

	“a”
A	B
C	B

 

	“b”
A	C
C	C

 

Como en este caso, para ambos valores, no se pudo partir el conjunto en otros conjuntos, => que A y C son estados que hacen el mismo trabajo => se pude eliminar alguno.

 

Se tiene lo siguiente

 

	“a”	“b”
=>A	B	C
B	B	D
C	B	C
D	B	E
**E	B	C

 

Se decide eliminar el estado C (arbitrariamente), entonces se reemplazan los estados C por el estado A.

 

Además, ya que he decidido eliminar C, y como C es un estado, se van TODOS los valores de su Fila

 

	“a”	“b”
=>A	B	A
B	B	D
D	B	E
**E	B	A

 

 

Como con TODAS las letras del alfabeto (del Autómata) no cae en particiones distintas => Terminé.

 

 

 

 

 

 

 

 

Bibliografía

 

[1] Aho, A.V., “Compiladores Principios, técnicas y herramientas”, Addison-Wesley Iberoamericana, Rading, Massachussets, E.U.A., 1986